Question

A rock weighs 110 N in air and has a volume of 0.00337 m3 . What is its apparent weight when submerged in water? The acceleration of gravity is 9.8 m/s 2 . Answer in units of N.

Answer 1

Step-by-step explanation:

It is given that,

Weight of the rock in air, W = 110 N

Since, W = mg

`m=(W)/(g)`

`m=(110\ N)/(9.8\ m/s^2)`

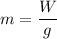
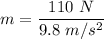
m = 11.22 kg

We need to find the apparent weight of the rock when it is submerged in water. Apparent weight is equal to the weight of liquid displaced i.e.

`M=d* V`

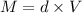
d is the density of water,
`d=1000\ kg/m^3`

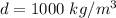
V is the volume of rock,
`V=0.00337\ m^3`

`M=1000\ kg/m^3* 0.00337\ m^3`

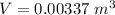
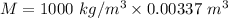
M = 3.37 kg

The apparent weight in water, W = m - M

`W=7.85\ kg* 9.8\ m/s^2`

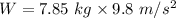
W = 76.93 N

So, the apparent weight of the rock is 76.93 N. Hence, this is the required solution.