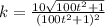Question

Use the alternative curvature formula K=|a x v|/|v|^3 to find the curvature of the following parameterized curves. to find the curvature of the following parameterized curve. r(t)=<6+5t^2, t, 0>

Answer 1

`k=\frac{10}{(100t^2+1)^{(3)/(2)}}`

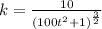
Or

`k=(10√(100t^2+1))/((100t^2+1)^(2))`

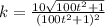
Explanation:

We want to compute the curvature of the parameterized curve,
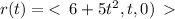`r(t)=\:<\:6+5t^2,t,0)\:>\:` using the alternative formula:

`k=(|a* v|)/(|v|^3)`.

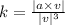We first compute the required ingredients.

The velocity vector is
`v=r'(t)=<\:10t,1,0\:>`

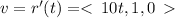
The acceleration vector is given by
`a=r''(t)=<\:10,0,0\:>`

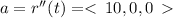
The magnitude of the velocity vector is
`|v|=√((10t)^2+1^2+0^2)=√(100t^2+1)`

The cross product of the velocity vector and the acceleration vector is

`a* v=\left|\begin{array}{ccc}i&j&k\\10&0&0\\10t&1&0\end{array}\right|=10k`

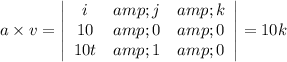
We now substitute ingredients into the formula to get:

`k=(|10k|)/((√(100t^2+1))^3)`.

`k=\frac{10}{(100t^2+1)^{(3)/(2)}}`

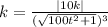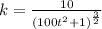
Or

`k=(10√(100t^2+1))/((100t^2+1)^(2))`