Question

the vertex of this parabola is at (-5,-2). when the x-value is -4, the y-value is 2. what is the coefficient of the squared term in the parabolas equation

Answer 1

First case The coefficient of the squared term is 4

Second case The coefficient of the squared term is 1/16

Explanation:

I will analyze two cases

First case (vertical parabola open upward)

we know that

The equation of a vertical parabola in vertex form is equal to

`y=a(x-h)^(2)+k`

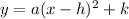
where

a is the coefficient of the squared term

(h,k) is the vertex

we have

(h,k)=(-5,-2)

substitute

`y=a(x+5)^(2)-2`

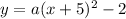
Find the value of a

Remember that

when the x-value is -4, the y-value is 2.

substitute

For x=-4, y=2

`2=a(-4+5)^(2)-2`

`2=a(1)-2`

`a=2+2=4`

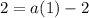
the equation is equal to

`y=4(x+5)^(2)-2`

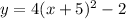
therefore

The coefficient of the squared term is 4

Second case (horizontal parabola open to the right)

we know that

The equation of a horizontal parabola in vertex form is equal to

`x=a(y-k)^(2)+h`

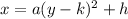
where

a is the coefficient of the squared term

(h,k) is the vertex

we have

(h,k)=(-5,-2)

substitute

`x=a(y+2)^(2)-5`

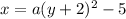
Find the value of a

Remember that

when the x-value is -4, the y-value is 2.

substitute

For x=-4, y=2

`-4=a(2+2)^(2)-5`

`-4=a(4)^(2)-5`

`-4+5=a(16)`

`a=1/16`

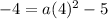
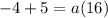
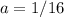
the equation is equal to

`x=(1/16)(y+2)^(2)-5`

therefore

The coefficient of the squared term is 1/16

to better understand the problem see the attached figure