Question

Suppose there is a pendulum with length 5m hanging from a ceiling. A ball of mass 2kg is attached is attached to the bottom of the pendulum. The ball begins at rest. If I give the ball a velocity of 6 m/s, what is the maximum height that the ball will achieve? Use the energy conservation model to solve, and assume that there is no friction or air resistance.

Answer 1

1.84 m from the initial point (3.16 m from the ceiling)

Step-by-step explanation:

According to the law of conservation of energy, the initial kinetic energy of the ball will be converted into gravitational potential energy at the point of maximum height.

Therefore, we can write:

`(1)/(2)mv^2 = mg\Delta h`

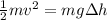
where

m = 2 kg is the mass of the ball

v = 6 m/s is the initial speed of the ball

g = 9.8 m/s^2 is the acceleration due to gravity

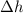`\Delta h` is the change in height of the ball

Solving for
`\Delta h`,

`\Delta h = (v^2)/(2g)=(6^2)/(2(9.8))=1.84 m`

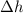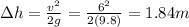
So, the ball raises 1.84 compared to its initial height.

Therefore:

- if we take the initial position of the ball as reference point, its maximum height is at 1.84 m

- if we take the ceiling as reference point, the maximum height of the ball will be

5 m - 1.84 m = 3.16 m from the ceiling