Question

SOS I need help with this question

Equation: 2x^2 + 10x - 3x - 15

Step1: Factor completely (10 points)

step2: after the polynomial is factored, solve the zeroes of the function

step3: describe the end behavior of the graph

step4: will the vertex of the function be minimum or maximum function?

Answer 1

1) (2x - 3)(x + 5)

2) 1.5, -5

3) Open upwards from both ends

4) Minimum

Explanation:

Step 1:

The given polynomial is:

`2x^(2)+10x-3x-15`

Taking out commons, we get:

`2x(x+5)-3(x+5)\\\\ =(2x-3)(x+5)`

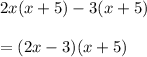
This is the factorized form of the polynomial.

Step 2:

The zeros of the functions occur when the function is equal to zero.

i.e.

`(2x-3)(x+5)=0\\\\ \text{According to the zero product property}\\\\ 2x-3=0, x+5=0\\\\ x =(3)/(2)=1.5, x = -5`

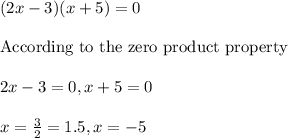
This means, the zeros of the polynomial are 1.5 and -5

Step 3:

The end behavior of a graph depends on its degree and the sign of leading coefficient. Since the degree is even and the coefficient is positive the graph of the polynomial will opens upwards from left and right side.

Step 4:

The given polynomial is a quadratic function with positive leading coefficient. Since it open vertically upwards, its vertex will be the lowest most point. So, the vertex will be the minimum of the function.