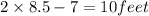Question

The floor of a shed given on the right has an area of 85 square feet. The floor is in the shape of a rectangle whose length is 7 feet less than twice the width. Find the length and the width of the floor of the shed.

Answer 1

The width of rectangular floor shed =8.5 feet

Length of rectangular floor shed=
`2*8.5-7=10 feet`

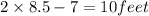
Explanation:

We are given that a floor is in rectangular shape.

We have to find the length and width of rectangular floor shed.

The area of floor shed=85 square feet

Let width of floor shed=x feet

Length of floor shed=(2 x-7 ) feet

Area of rectangle=
`length* breadth`

According to question

Area of rectangular floor shed=
`x* (2x-7)`

`x(2x-7)=85`

`2x^-7x-85=0`

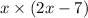
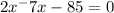
It is a quadratic equation

Using factorization method

`2x^2-17 x+10 x-85=0`

`x(2x-17)+5 (2 x-170)=0`

`(2x-17)(x+5)=0`

`x=(17)/(2) =8.5 and x=-5`

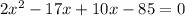
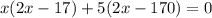
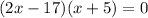
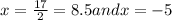
x=-5 is not possible because length and breadth of rectangle are always a natural number .

Therefore, the width of rectangular floor shed =8.5 feet

Length of rectangular floor shed=
`2*8.5-7=10 feet`

Answer 2

Answer: Length = 10 feet and width = 8.5 feet.

Explanation:

Let x be the width of the floor.

Then length of the floor =
`2x-7`

Given : The area of the floor = 85 square feet

We know that the area of a rectangle is given by :-

`A=l* w`

`\Rightarrow\ 85=(2x-7)* x\\\\\Rightarrow\ 2x^2-7x-85=0\\\\\ x=(-b\pm√(b^2-4ac))/(2a)\\\\\Rightarrow\ x=(7\pm√(49-4(2)(-85)))/(4)\\\\\Rightarrow\ x=(7\pm27)/(4)\\\\\Rightarrow\ x=(17)/(2), -5`

But dimension cannot be negative

So, the width of the floor =
`x=(17)/(2)=8.5\text{ feet}`

And the length of the floor =
`2(8.5)-7=10\text{ feet}`