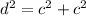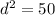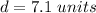Question

In the figure, a square is inside another bigger square.

If a = 4 units and b = 3 units, the length of the diagonal of the outside square rounded to the nearest tenth is _____
units and the length of the diagonal of the inside square rounded to the nearest tenth is _____ units.

Answer 1

Part 1) The length of the diagonal of the outside square is 9.9 units

Part 2) The length of the diagonal of the inside square is 7.1 units

Explanation:

step 1

Find the length of the outside square

Let

x -----> the length of the outside square

c ----> the length of the inside square

we know that

`x=a+b=4+3=7\ units`

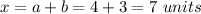
step 2

Find the length of the inside square

Applying the Pythagoras Theorem

`c^(2)= a^(2)+b^(2)`

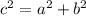
substitute

`c^(2)= 4^(2)+3^(2)`

`c^(2)=25`

`c=5\ units`

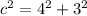
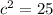
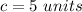
step 3

Find the length of the diagonal of the outside square

To find the diagonal Apply the Pythagoras Theorem

Let

D -----> the length of the diagonal of the outside square

`D^(2)= x^(2)+x^(2)`

`D^(2)= 7^(2)+7^(2)`

`D^(2)=98`

`D=9.9\ units`

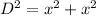
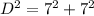
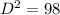
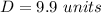
step 4

Find the length of the diagonal of the inside square

To find the diagonal Apply the Pythagoras Theorem

Let

d -----> the length of the diagonal of the inside square

`d^(2)= c^(2)+c^(2)`

`d^(2)= 5^(2)+5^(2)`

`d^(2)=50`

`d=7.1\ units`