Question

The coordinates G(7, 3), H(9, 0), I(5, -1) form what type of polygon?

an obtuse triangle

Answer 1

Is an acute triangle

Explanation:

we have

`G(7, 3),H(9, 0),I(5, -1)`

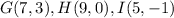
so

The polygon is a triangle

we know that

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

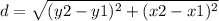
Remember that

If applying the Pythagoras Theorem

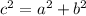`c^(2)=a^(2)+b^(2)` -----> is a right triangle

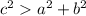`c^(2)>a^(2)+b^(2)` -----> is an obtuse triangle

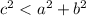`c^(2)<a^(2)+b^(2)` -----> is an acute triangle

where

c is the greater side

step 1

Find the distance GH

`G(7, 3),H(9, 0),I(5, -1)`

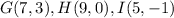
substitute

`d=\sqrt{(0-3)^(2)+(9-7)^(2)}`

`d=\sqrt{(-3)^(2)+(2)^(2)}`

`GH=√(13)\ units`

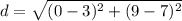
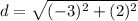
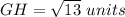
step 2

Find the distance HI

`G(7, 3),H(9, 0),I(5, -1)`

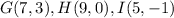
substitute

`d=\sqrt{(-1-0)^(2)+(5-9)^(2)}`

`d=\sqrt{(-1)^(2)+(-4)^(2)}`

`HI=√(17)\ units`

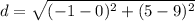
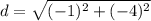
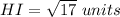
step 3

Find the distance GI

`G(7, 3),H(9, 0),I(5, -1)`

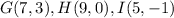
substitute

`d=\sqrt{(-1-3)^(2)+(5-7)^(2)}`

`d=\sqrt{(-4)^(2)+(-2)^(2)}`

`GI=√(20)\ units`

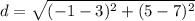
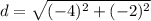
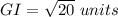
step 4

Let

`c=GI=√(20)\ units`

`a=HI=√(17)\ units`

`b=GH=√(13)\ units`

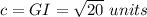
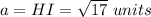
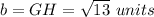
Find
`c^(2)` ------>
`c^(2)=(√(20))^(2)=20`

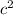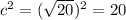
Find
`a^(2)+b^(2)` ---->
`(√(17))^(2)+(√(13))^(2)=30`

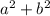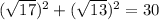
Compare

`20 < 30`

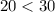
therefore

Is an acute triangle