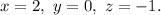Question

Find the solution to this system of equations

3x+2y+3z=3 4x-5y+7z=1 2x+3y-2z=6
x=? Y=? Z=?

Answer 1

3x + 2y + 3z = 3

4x − 5y + 7z = 1

2x + 3y − 2z = 6

x =

2

y =

0

z =

-1

Explanation:

Plato!

Answer 2

The solution is
`x=2,\ y=0,\ z=-1.`

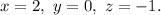
Explanation:

You are given the system of three equations:

`\left\{\begin{array}{l}3x+2y+3z=3\\4x-5y+7z=1\\2x+3y-2z=6\end{array}\right.`

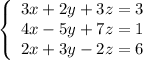
Multiply the first equation by 4, the second equation by 3 and subtract them. Then multiply the third equation by 2 and subtract it from the second equation:

`\left\{\begin{array}{l}3x+2y+3z=3\\4(3x+2y+3z)-3(4x-5y+7z)=4\cdot 3-3\cdot 1\\4x-5y+7z-2(2x+3y-2z)=1-2\cdot 6\end{array}\right.\Rightarrow \\\\\left\{\begin{array}{l}3x+2y+3z=3\\12x+8y+12z-12x+15y-21z=12-3\\4x-5y+7z-4x-6y+4z=1-12\end{array}\right.`

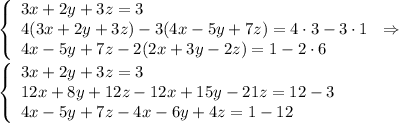
So,

`\left\{\begin{array}{rl}3x+2y+3z=3\\23y-9z=9\\-11y+11z=-11\end{array}\right.\Rightarrow \left\{\begin{array}{l}3x+2y+3z=3\\23y-9z=9\\y-z=1\end{array}\right.`

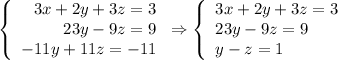
Multiply the third equation by 23 and subtract it from the second equation:

`\left\{\begin{array}{rl}3x+2y+3z=3\\23y-9z=9\\23y-9z-23(y-z)=9-23\cdot 1\end{array}\right.\Rightarrow \left\{\begin{array}{rl}3x+2y+3z=3\\23y-9z=9\\23y-9z-23y+23z=9-23 \end{array}\right.`

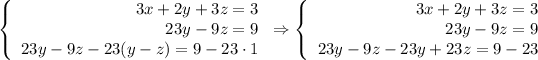
Hence,

`\left\{\begin{array}{rl}3x+2y+3z=3\\23y-9z=9\\14z=-14 \end{array}\right.\Rightarrow z=-1`

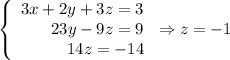
Substitute it into the second equation:

`23y-9\cdot (-1)=9\Rightarrow 23y+9=9\\ \\23y=0\\ \\y=0`

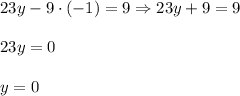
Substitute them into the first equation:

`3x+2\cdot 0+3\cdot (-1)=3\Rightarrow 3x-3=3\\ \\3x=6\\ \\x=2`

The solution is
`x=2,\ y=0,\ z=-1.`