Question

The slope of MN is −3. Which segments are parallel to MN ? Select each correct answer.

A= RS, where R is at (1, 3) and S is at (4, 2)

B= PQ, where P is at (5, 6) and Q is at (8, 7)

C= TU, where T is at (8, 1) and U is at (5, 10)

D= WX, where W is at (2, 6) and X is at (4, 0)
Report by TurtleAnderson

Answer 1

Option C and D is correct

Explanation:

We need to find the slopes of the given segments.

The lines are parallel if there slopes are equal.

A) = RS, where R is at (1, 3) and S is at (4, 2)

`Slope\,\,of\,\,RS =(y_(2)-y_(1))/(x_(2)-x_(1)) \\Slope\,\,of\,\,RS=(2-3)/(4-1)\\Slope\,\,of\,\,RS=(-1)/(3)`

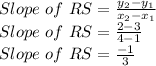
Option A is incorrect because Slope of MN = -3 while slope of RS = -1/3

B)= PQ, where P is at (5, 6) and Q is at (8, 7)

`Slope\,\,of\,\,PQ =(y_(2)-y_(1))/(x_(2)-xx_(1)) \\Slope\,\,of\,\,PQ=(7-6)/(8-5)\\Slope\,\,of\,\,PQ=(1)/(3)`

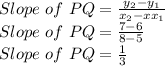
Option B is incorrect because Slope of MN = -3 while slope of PQ = 1/3

C)= TU, where T is at (8, 1) and U is at (5, 10)

`Slope\,\,of\,\,TU=(y_(2)-y_(1))/(x_(2)-xx_(1)) \\Slope\,\,of\,\,TU\,\,=(10-1)/(5-8)\\Slope\,\,of\,\,TU\,\,=(9)/(-3) \\Slope\,\,of\,\,TU=-3`

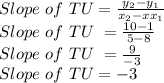
Option C is correct because Slope of MN = -3 while slope of TU = -3

D)= WX, where W is at (2, 6) and X is at (4, 0)

`Slope\,\,of\,\,WX\, =(y_(2)-y_(1))/(x_(2)-xx_(1)) \\Slope\,\,of\,\,WX\,=(0-6)/(4-2)\\Slope\,\,of\,\,WX\,=(-6)/(2) \\Slope\,\,of\,\,WX\,=-3`

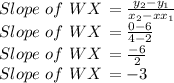
Option D is correct because Slope of MN = -3 while slope of WX = -3