Question

2.42. Consider f (x) = x3????x and g(x) = x2????1 on x 2 [????1;1]. (a) Verify that f (x) is an odd function and g(x) is an even function, meaning f (????x) = ????f (x)) and g(????x) = g(x). (b) Directly compute that h f (x);g(x)i = 0.

Answer 1

f(x) is an odd function and g(x) is an even function

Explanation:

Even Function :

A function f(x) is said to be an even function if

f(-x) = f(x) for every value of x

Odd Function :

A Function is said to be an odd function if

f(-x)= -f(x)

Part a)

`f(x)=x^3+x`

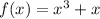
let us substitute x with -x

`f(-x) = (-x)^3-x\\=-x * -x * -x\\=-x^3-x\\=-(x^3+x)\\=-f(x)`

Hence

f(-x)=-f(x)

There fore f(x) is an odd function

`g(x)=x^2+1`

Substituting x with -x we get

`g(-x)=(-x)^2+1\\=-x * -x+1\\=x^2+1\\=g(x)`

Hence g(-x)=g(x)

Therefore g(x) is an even Function.

Part b)

hf(x)=hx^3