Question

When the components arrive, the company selects a random sample from the shipment and subjects the selected components to a rigorous set of tests to determine if the components in the shipments conform to their specifications. From a recent large shipment, a random sample of 250 of the components was tested, and 24 units failed one or more of the tests. What is the 95% confidence interval estimate for the true proportion of components, p, that fail to meet the specifications

Answer 1

(0.059, 0.133)

Explanation:

Sample size = n = 250

Number of units which failed the test = x = 24

Proportion of units which failed the test =
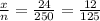`(x)/(n) = (24)/(250) =(12)/(125)` = 0.096

Proportion of units which did not fail the test = q = 1 - p = 1 - 0.096 = 0.904

Confidence level = 95%

z-value for the confidence level = z = 1.96

The true proportion of the components that fail to meet the specification would be:

`(p-z\sqrt{(p * q)/(n)} , p+z\sqrt{(p * q)/(n)})`

Using the values, we get:

`(0.096-1.96 * \sqrt{(0.096 * 0.904)/(250)} , 0.096+1.96 * \sqrt{(0.096 * 0.904)/(250)})\\\\ =(0.059,0.133)`

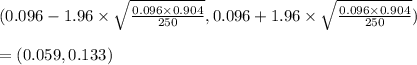
Thus, 95% confidence interval estimate for the true proportion of components, p, that fail to meet the specifications is (0.059, 0.133)