Question

A 10-cm-long spring is attached to the ceiling. When a 2.0 kg mass is hung from it, the spring stretches to a length of 15 cm.?A) What is the spring constant k? B) How long is the spring when a 3.0 kg mass is suspended from it?

Answer 1

A) 392 N/m

The spring constant can be found by applying Hooke's Law:

F = kx

where

F is the force applied to the spring

k is the spring constant

x is the stretching of the spring

Here we have:

F is the weight of the block hanging from the spring, which is

`F=mg=(2.0 kg)(9.8 m/s^2)=19.6 N`

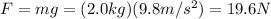
The stretching of the spring is

`x=15 cm - 10 cm = 5 cm = 0.05 m`

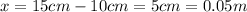
Therefore its spring constant is

`k=(F)/(x)=(19.6 N)/(0.05 m)=392 N/m`

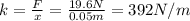
B) 17.5 cm

Now that we know the value of the spring constant, we can calculate the new stretching of the spring when a mass of m=3.0 kg is applied to it. In this case, the force applied on the spring is

`F=mg=(3.0 kg)(9.8 m/s^2)=29.4 N`

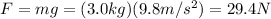
Therefore the stretching of the spring is

`x=(F)/(k)=(29.4 N)/(392 N/m)=0.075 m = 7.5 cm`

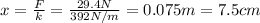
And since the natural length of the spring is 10 cm, the new length will be

L = 10 cm + 7.5 cm = 17.5 cm