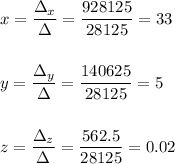Answer:
Gold - $33, Silver - $5, Copper - $0.02
Explanation:
Let $x be the price of one gram of gold, $y - price of 1 g of silver and $z - price of 1 g of copper.
1. The first alloy is 75% gold, 5% silver, and 20% copper, so in 100 g there are 75 g of gold, 5 g of silver and 20 g of copper. If 100 g of the first alloy costs $2500.40, then
75x+5y+20z=2500.40
2. The second alloy is 75% gold, 12.5% silver, and 12.5% copper, so in 100 g there are 75 g of gold, 12.5 g of silver and 12.5 g of copper. If 100 g of the first alloy costs $2537.75, then
75x+12.5y+12.5z=2537.75
3. The third alloy is 37.5% gold and 62.5% silver, so in 100 g there are 37.5 g of gold and 62.5 g of silver . If 100 g of the first alloy costs $1550.00, then
37.5x+62.5y=1550.00
Solve the system of three equations:
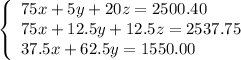
Find all determinants
![\Delta=\|\left[\begin{array}{ccc}75&5&20\\75&12.5&12.5\\37.5&62.5&0\end{array}\right] \|=28125\\ \\</p><p>\Delta_x=\|\left[\begin{array}{ccc}2500.40&5&20\\2537.75&12.5&12.5\\1550.00&62.5&0\end{array}\right] \|=928125\\ \\</p><p>\Delta_y=\|\left[\begin{array}{ccc}75&2500.40&20\\75&2537.75&12.5\\37.5&1550&0\end{array}\right] \|=140625\\ \\</p><p>\Delta_z=\|\left[\begin{array}{ccc}75&5&2500.40\\75&12.5&2537.75\\37.5&62.5&1550\end{array}\right] \|=562.5\\ \\](https://img.qammunity.org/2020/formulas/mathematics/college/y5042ib00rae76wkw80rjmd4lg5ervwpno.png)
So,