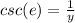Answer:
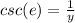
Explanation:
It is given that the point P(x, y) lies on the unit circle and is defined by real number e. We have to find csc(e) i.e cosecant of (e)
This scenario is represented in the figure attached below.
The formula of csc is:
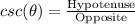
A right angled triangle is constructed, as shown in figure. The hypotenuse of the triangle forms the radius of the circle. Since, the circle is a unit circle the length of hypotenuse would be equal to 1.
Hypotenuse = 1
So, the formula of csc would be reduced to:
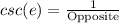
The side opposite to the angle made at origin is y. So,