Question

Express the confidence interval left parenthesis 0.023 comma 0.085 right parenthesis(0.023,0.085) in the form of ModifyingAbove p with caret minus Upper E less than p less than ModifyingAbove p with caret plus Upper Ep−E

Answer 1

(0.054 - 0.031, 0.054 + 0.031)

Explanation:

We are given the confidence interval of the population proportion and we have to express it in terms of p - E and p + E, where p is the sample proportion and E is the margin of error.

Sample proportion(p) is calculated as the average of the lower limit and upper limit of the confidence interval. Lower limit of the confidence interval is 0.023 and the upper limit is 0.085. So,

`p = (0.085+0.023)/(2)=0.054`

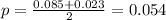
This gives us the value of p.

Margin of Error(E) is half of the difference of upper and lower limit of the confidence interval. So,

`E=(0.085-0.023)/(2)=0.031`

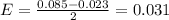
Now, the given confidence interval can be expressed as:

(0.054 - 0.031, 0.054 + 0.031)