Question

Assume that the heights of adult Caucasian women have a mean of 63.6 inches and a standard deviation of 2.5 inches. If 100 women are randomly​ selected, find the probability that they have a mean height greater than 63.0 inches. Round to four decimal places.A.0.9918B.0.8989C.0.2881D.0.0082E. not enough information to determine

Answer 1

A. 0.9918

Explanation:

Mean Height = u = 63.6 inches

Standard deviation =
`\sigma` = 2.5 inches

Sample size = 100

We have to find the probability that the mean height of sample would be greater than 63 i.e. P(x > 63)

We can do this by converting this value to z-score.

The formula to find z-score given the mean, standard deviation and sample size is:

`z=(x-u)/((\sigma)/(√(n)))`

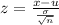
Using the values, we get:

`z=(63-63.6)/((2.5)/(√(100) ) )\\\\ z=-2.4`

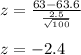
So now we have to find the probability that the z score would be greater than -2.4

i.e. P(z > -2.4)

From the z-table this value comes out to be:

P(z > -2.4) = 0.9918

Since,

P ( x > 63.0) is equivalent to P(z > -2.4), we can say:

P( x > 63.0 ) = 0.9918

Thus, the probability that adult Caucasian women have a mean height greater than 63.0 inches is 0.9918