Question

A certain radioactive isotope decays according to the formula A = A0e − 0.0242 t , where A0 is the amount of the isotope initially present, and A is the amount present after t years. Approximately how many years will have to pass before only 50 % of a particular quantity of the isotope remains. Your answer will be the half-life of the isotope. Round to 3 decimal places.

Answer 1

• 28.642 years

Step-by-step explanation:

1) Radioactive decay equation (given):

• 
  `A=A_0e^(-0.0242t)`

2) Half-life of the isotope:

As stated the concentration after the half-life time is 50%. So, you can use A = A₀ / 2 and solve for t:

`A=A_0e^(-0.0242t)\\ \\ A/A_0=1/2=e^(-0.0242t)\\ \\-0.0242t=ln(1/2)\\ \\0.0242t=ln2\\ \\ t=ln2/0.0242= 28.642`

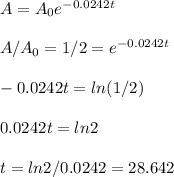
Thus, the answer, rounded to 3 decimal places as requested, is 28.642 years, and that is the half-life of the isotope.