Question

Which of the following is a polynomial with roots negative square root of 5, square root of 5, and 3?

Answer 1

`x^(3)-3x^(2)-5x+15`

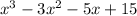
Explanation:

The roots of the given polynomial are:
`-√(5), √(5), 3`

Since,
`-√(5), √(5), 3` are the roots of the polynomial, according to the factor theorem,
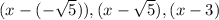`(x - (-√(5))), (x-√(5)), (x-3)` would be the factors of the polynomial.

Since we have the factors of the polynomial, we can multiply them to get the desired polynomial.

Let the polynomial be represented by P(x), so

`P(x) = (x - (-√(5)))(x-√(5))(x-3)\\\\ P(x)=(x +√(5))(x-√(5))(x-3)\\\\ P(x)=(x^(2)-(√(5) )^(2))(x-3)\\\\ P(x)=(x^(2)-5)(x-3)\\\\ P(x)=x^(3)-3x^(2)-5x+15`

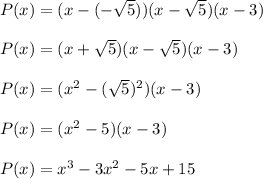
The polynomial represented by P(x) has the given roots.