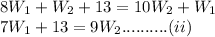Question

There are two piles, one containing 9gold coins and the other 11silver coins. The two piles of coins weigh the same. One coin is taken from each pile and put into the other. It is now found that the pile of mainly gold coins weighs 13units less than the pile of mainly silver coins. Let x represent the weight of each gold coin and y the weight of each silver coin. Find the weight of a silver coin and of a gold coin.

Answer 1

Weight of silver coin = 29.25 units , weight of gold coin = 35.75 units

Step-by-step explanation:

Let the weight of 1 gold coin be
`W_(1)`

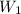
Weight of 1 silver coin be
`W_(2)`

Total no of gold coins = 9

Total no of silver coins = 11

Total weight of gold coins = 9
`* W_(1)`

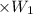
Total weight of silver coins = 11
`* W_(2)`

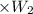
It is given that both weigh same thus we have

`9W_(1)=11W_(2)............(i)`

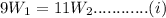
After replacing coins the weights become as under

`Gold Stack\\9W_(1)-W_(1)+W_(2)=8W_(1)+W_(2)\\\\SilverStack\\\\11W_(2)-W_(2)+W_(1)=10W_(2)+W_(1)`

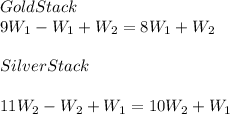
Now it is given that gold stack weighs 13 unit less thus adding 13 units to gold stack gives it's weight equal to silver stack

the above relation modifies as

`8W_(1)+W_(2)+13=10W_(2)+W_(1)\\7W_(1)+13=9W_(2)..........(ii)`

`8W_(1)+W_(2)+13=10W_(2)+W_(1)\\7W_(1)+13=9W_(2)..........(ii)\\\\7\frac{11W_(2)}\\\\Solving equation i and ii we get\\\\{9}+13=9W_(2)\\\\77W_(2)+117=81W_(2)\\\\4W_(2)=117\\\\W_(2)=(117)/(4)=29.25units\\\\W_(1)=(11W_(2))/(9)=35.75units`