Question

In a lottery​ game, the jackpot is won by selecting five different whole numbers from 1 through 37 and getting the same five numbers​ (in any​ order) that are later drawn. In the Pick 5 ​game, you win a straight bet by selecting five digits​ (with repetition​ allowed), each one from 0 to​ 9, and getting the same five digits in the exact order they are later drawn. The Pick 5 game returns ​$50,000 for a winning​ $1 ticket. Complete parts​ (a) through​ (c) below:a. In a lottery​ game, the jackpot is won by selecting fivefive different whole numbers from 1 through 37 and getting the same five numbers​ (in any​ order) that are later drawn. What is the probability of winning a jackpot in this​ game? ​P(winning a jackpot in this ​game)=b. In the Pick 5 ​game, you win a straight bet by selecting five digits​ (with repetition​ allowed), each one from 0 to​ 9, and getting the same five digits in the exact order they are later drawn. What is the probability of winning this​ game? ​P(winning the Pick 55​game)=c. The Pick 5 game returns ​$50,000 for a winning​ $1 ticket. What should be the return if the lottery organization were to run this game for no​ profit? ​

Answer 1

a. In the lottery game, it seems that repetition of numbers getting picked is *not* allowed. There are

`\dbinom{37}5=(37!)/(5!(37-5)!)=435,897`

ways of picking any 5 numbers between 1 and 37, so the probability of winning the jackpot is 1/435,897.

b. With repetition allowed, there are

`10^5=100,000`

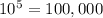
possible ways to draw any 5 numbers between 0 and 9, so the probability of winning the jackpot is 1/100,000.

c. In order for the game to be no-profit, its expected value should be 0. This basically means that the amount of money players pay to play the game should be balanced exactly by the winning amount. If
`X` represents the amount of money won by a player, then

`X=\begin{cases}-1&\text{if the picked numbers do not match}\\49,999&\text{if the picked numbers do match}\end{cases}`

with probabilities

`P(X=x)=\begin{cases}(99,999)/(100,000)&\text{for }X=-1\\\frac1{100,000}&\text{for }X=49,999\end{cases}`

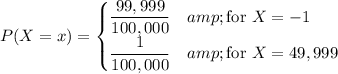
The expected value is

`E[X]=\displaystyle\sum_xx\,P(X=x)=-(99,999)/(100,000)+(49,999)/(100,000)=-\frac12`

which means the average player is expected to lose $0.50.

The game is no-profit if the jackpot is
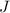`J` such that

`E[X]=-(99,999)/(100,000)+(J-1)/(100,000)=0`

Solving for
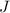`J` tells us the jackpot should be $100,000.