Question

A piston–cylinder device contains 0.85 kg of refrigerant134a at –10°C. The piston that is free to move has a mass of 12 kg and a diameter of 25 cm. The local atmospheric pressure is 88 kPa. Now, heat is transferred to refrigerant-134a until the temperature is 15°C. Determine (a) the final pressure, (b) the change in the volume of the cylinder, and (c) the change in the enthalpy of the refrigerant-134a.

Answer 1

To solve the student's problem involving refrigerant-134a, specific thermodynamic properties are required, and without them, determining the final pressure, volume change, and enthalpy change is not possible.

Step-by-step explanation:

The student's question involves an initial state of refrigerant-134a in a piston-cylinder device and a process where heat is added and changes the state to a higher temperature. The information required to solve this problem typically involves the principles of thermodynamics, and specifically the relationships between pressure, volume, temperature, and enthalpy of a substance.

To determine the final pressure (a), one would normally apply the ideal gas law or real gas equations, if available for the specific refrigerant. However, without specific properties of refrigerant-134a at the given temperatures, or the final state of the refrigerant (liquid, vapor, or a mixture), the problem remains unsolvable.

Similarly, the change in the volume of the cylinder (b) and the change in enthalpy (c) would require more detailed property data of refrigerant-134a and may also depend on whether the piston's motion is restrained or not by external forces that are not accounted for by atmospheric pressure alone.

Without this additional data or specifics on the refrigerant states, we cannot provide a definitive solution to the student’s question.

Answer 2

a) 90.40 kPa

b) ΔV=0.0220
`m^(3)`

c) ΔH=17.42 kJ

Step-by-step explanation:

As R-134a is a simple fluid, we just need 2 thermodynamic properties to know its state. For the initial state, we know the temperature, and we can calculate the pressure.

Pressure calculation:

If the piston-cylinder system is under atmospheric pressure, the pressure inside the the system may be the sum of the atmospheric pressure plus the pressure that is made by the piston weight:

Piston weight:
`W=m*g=12kg*9.81(m)/(s^(2))=117.72N=0.11772kN`

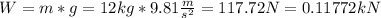
This weight is supported by the fluid through an area of:

`A=(\pi d^(2))/(4) =(\pi 0.25^(2))/(4)=0.0491m^(2)`

So the pressures that the piston exert over the fluid is:
`P=(F)/(A) =(W)/(A)=(0.11772kN)/(0.0491m^(2))=`

So, the total pressure will be:

`P=88kPa+2.398kPa=90.40kPa`

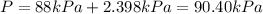
Volume change

The pressure calculated before is constant because the system is not rigid and the atmospheric pressure and the piston pressure does not change. So, knowing temperature and pressure, it is possible to know the specific volume of the fluid by means of the steam tables.

The initial volume is the volume estimated at T=-10ºC and P=90.40 kPa. We realize that it is a superheated vapor because the pressure is a higher than the saturation one. We will have to make an interpolation for several data.

The interpolation for the volume is:
`v_(1) =0.2488(m^(3))/(kg)`

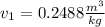
For the final volume (T=15ºC, P=90.40kPa) it will be required a double interpolation, which result is:
`v_(2)=0.2747(m^(3))/(kg)`

The change in the volume will be:

`V_(2)-V_(1) =m*(v_(2)-v_(1))=0.85*(0.2747-0.2488)=0.0220m^(3)`

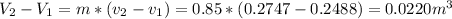
Enthalpy Change

For the enthalpy change we apply the same process, being the interpolation results:

`h_(1)=395.53(kJ)/(kg)\\h_(2)=416.05(kJ)/(kg)`

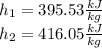
So, the total enthalpy change is:

`H_(2)-H_(1) =m*(h_(2)-h_(1))=0.85*(416.05-395.53)=17.42kJ`

Note: The steam tables used was the tables from van Wylen, 6 edition, table B.5.2