Question

Question 2 of 10

2 Points
True or False? The opposite angles of a quadrilateral in a circumscribed circle
are always complementary.
O
A. True
O
B. False
SUBMIT

Answer 1

Answer: False

Explanation:

a pex correct answer is false

Answer 2

Choice B. False. Rather, the opposite angles of a circumscribed quadrilateral are always supplementary with a sum of 180 degrees.

Explanation:

Refer to the sketch attached.

Consider the quadrilateral ABCD inscribed in the circle O. Angle
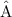`\mathrm{\hat{A}}` is the angle that line BA and DA inscribe. The green angle at O will be the arc that the two lines intercepts. Let angle A equals
`\alpha` degrees. By the inscribed angle theorem for circles, The green angle will measure
`\rm 2\hat{A} = 2\alpha`.

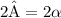Similarly, the arc that line CD and CB intercept will equal to twice the measure of
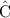`\rm \hat{C}`. The angle of that arc is the red angle at the origin. The value of that arc will equal to
`360\textdegree{} - 2\alpha`.

Angle
`\hat{C}` is half the measure of that arc. That is:

`\rm \displaystyle \hat{C} = (1)/(2) (360 \textdegree - 2\alpha) = 180 - \alpha`.

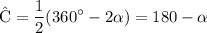Note that
`\rm \hat{A} + \hat{C} = \alpha + (180\textdegree - \alpha) = 180\textdegree`. The sum of A and angle C is 180 degrees. In other words, the two angles are supplementary. The claim that the two angles are complementary (which describes two angles with a sum of 90 degrees) will thus be false.