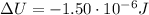Question

A particle with a charge of +4.50 nC is in a uniform electric field E+ directed to the negative x direction. It is released from rest, and after it has moved 8.00 cm , its kinetic energy is found to be 1.50×10^−6 J . You may want to review (Pages 567 - 572) . For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Parallel plates and conservation of energy.

Part A: What work was done by the electric force?Part B: What was the change in electric potential over the distance that the charge moved?Part C: What is the magnitude of E+ ?Part D: What was the change in potential energy of the charge?

Answer 1

(a)
`1.50\cdot 10^(-6)J`

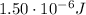
According to the work-energy theorem, the work done by the electric force is equal to the kinetic energy gained by the particle, so we can write:

`W=K_f - K_i`

where

W is the work done by the electric force

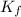`K_f` is the final kinetic energy of the particle

`K_i` is the initial kinetic energy of the particle

Since the particle starts from rest,
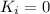`K_i = 0`. Moreover,

`K_f = 1.50\cdot 10^(-6)J`

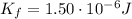
Therefore, the work done by the electric force is

`W=K_f = 1.50\cdot 10^(-6)J`

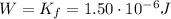
(b) -333.3 V

According to the law of conservation of energy, the gain in kinetic energy of the particle must correspond to a loss in electric potential energy, so we can write:

`\Delta K = -\Delta U`

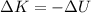
Where

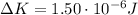`\Delta K = 1.50\cdot 10^(-6) J` is the gain in kinetic energy

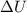`\Delta U` is the loss in electric potential energy

So we have

`\Delta U = - \Delta K = -1.50\cdot 10^(-6)J`

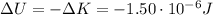
The loss in electric potential energy can be rewritten as

`\Delta U = q \Delta V`

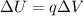
where

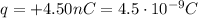`q=+4.50 nC = 4.5\cdot 10^(-9) C` is the charge of the particle

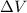`\Delta V` is the change in electric potential over the distance the charge has moved

Solving for
`\Delta V`,

`\Delta V= (\Delta U)/(q)=(-1.50\cdot 10^(-6))/(4.5\cdot 10^(-9))=-333.3 V`

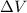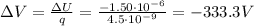
(c) 4166 V/m

The magnitude of the electric field is given by

`E=(|\Delta V|)/(d)`

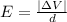
where

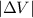`|\Delta V|` is the magnitude of the change in electric potential

d is the distance through which the charge has moved

Since we have

`|\Delta V|=333.3 V\\d = 8.00 cm = 0.08 m`

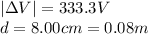
The magnitude of the electric field is

`E=(333.3)/(0.08)=4166 V/m`

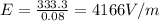
(d)
`-1.50\cdot 10^(-6)J`

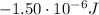
The change in electric potential energy of the charge has already been calculated in part (b), and it is

`\Delta U = -1.50\cdot 10^(-6)J`