Question

A study of 420 comma 100 cell phone users found that 133 of them developed cancer of the brain or nervous system. Prior to this study of cell phone​ use, the rate of such cancer was found to be 0.0449​% for those not using cell phones. Complete parts​ (a) and​ (b). a. Use the sample data to construct a 95​% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system.

Answer 1

(0.0263%, 0.0370%)

Explanation:

Sample size = n = 420,100

Number of users who developed cancer = x = 133

Proportion of users who developed cancer = p =
`(133)/(420100)`

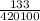
Proportion of users who didnot develop cancer = q = 1 - p =
`1-(133)/(420100)=(419967)/(420100)`

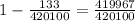
Confidence Level = 95%

Z value associated with this confidence level = z = 1.96

The formula to calculate the confidence interval is:

`\text{Lower Bound} = p-z\sqrt{(pq)/(n)}\\\\ \text{Upper Bound} = p+z\sqrt{(pq)/(n)}`

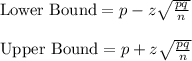
Using the values in above expressions, we get:

`\text{Lower Bound}=(133)/(420100)-1.96\sqrt{((133)/(420100)*(419667)/(420100))/(420100)}\\\\\text{Lower Bound}=0.000263`

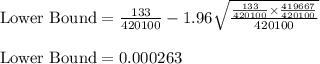
and

`\text{Upper Bound}=(133)/(420100)+1.96\sqrt{((133)/(420100)*(419667)/(420100))/(420100)} \\\\ \text{Upper Bound}=0.000370`

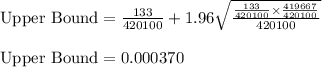
Thus, the bounds of the confidence interval are:

(0.000263, 0.000370)

This can be expressed in percentages as:

(0.0263%, 0.0370%)

Therefore, a 95​% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system is (0.0263%, 0.0370%)