Question

The mayor is interested in finding a 95% confidence interval for the mean number of pounds of trash per person per week that is generated in city. The study included 120 residents whose mean number of pounds of trash generated per person per week was 31.5 pounds and the standard deviation was 7.8 pounds. What is the confidence interval for the mean number of lbs of trash per person per week that is generated in the city?

Answer 1

very good answer

Explanation:

Answer 2

(30.09, 32.91)

Explanation:

Mean number of pounds of trash = x = 31.5 pounds

Standard deviation = s = 7.8 pounds

Sample size = n = 120

Confidence level = 95%

Since, we are given the sample standard deviation instead of the population standard deviation, we will use t-test to find the confidence interval.

Degrees of freedom = df = n - 1 = 120 - 1 = 119

The t-value associated with 95% confidence interval and df=119 from the t-table comes out to be:

t = 1.98

The formula to calculate the confidence interval is:

`(x-t(s)/(√(n)), x+t(s)/(√(n)))\\`

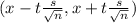
Using the values in above expression we get:

`(31.5-1.98*(7.8)/(√(120)), 31.5+1.98*(7.8)/(√(120)))\\\\ =(30.09,32.91)`

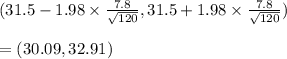
Thus, the 95% confidence interval for the mean number of lbs of trash per person per week that is generated in the city is (30.09, 32.91)