Question

Help would be much appreciated!!

Answer 1

a) AC = 11.4 cm

b) BC = 30.9 cm

Explanation:

Part a)

Consider the triangle ACD. We have two sides and an included angle and we have to find the side opposite to this angle. We can use the law of cosine to solve this problem. Let the side AC be referred to as "c", side AD be termed as "a" and side CD be termed as "b", According to the law of cosines:

`c^(2)=a^(2)+b^(2)-2abcos(\theta)`

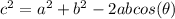
Using the values, we get:

`c^(2)=(17)^(2)+(13)^(2)-2(17)(13)cos(42)\\\\ c^(2)=129.53\\\\ c=√(129.53)\\\\ c=11.4`

Hence, we have shown that measure of side AC is 11.4 cm

Part b)

Consider the triangle ABC. We have two angles, a side and we need to find the side opposite to one of the given angles. This can be solved using the Law of sines.

Using the law of sines for given triangle, we get:

`(BC)/(sin(A))=(AC)/(sin(B))`

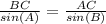
Since, we have two angles from triangles ABC, and sum of all angles should be 180, so we can write:

A + B + C = 180

76 + B + 83 = 180

B = 21

Using the values in law of sines, we get:

`(BC)/(sin(76))=(11.4)/(sin(21))\\\\ BC=(11.4)/(sin(21)) * sin(76)\\\\ BC = 30.9`

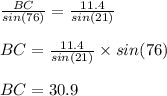
Thus, the measure of side BC would be 30.9 cm