Question

Model rocket engines are rated by the impulse that they deliver when they fire. A particular engine is rated to deliver an impulse of 3.5 kg⋅m/s. The engine powers a 140g rocket, including the mass of the engine. Part A What is the final speed of the rocket once the engine has fired? (Ignore the change in mass as the engine fires and ignore the weight force during the short duration of the engine firing.) Express your answer with the appropriate units.

Answer 1

v = 25 m/s

Step-by-step explanation:

It is given that,

A particular engine is rated to deliver an impulse of 3.5 kg⋅m/s, J = 3.5 kg⋅m/s

Mass of the rocket, m = 140 g = 0.14 kg

Initial speed of the rocket, u = 0

Let v is the final speed of the rocket once the engine is fired. We know that the change in momentum is equal to the impulse. Its expression is given by :

`J=m(v-u)`

`J=mv`

`v=(J)/(m)`

`v=(3.5\ kg-m/s)/(0.14\ kg)`

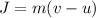
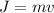
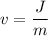
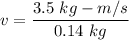
v = 25 m/s

So, the speed of the rocket is 25 m/s. Hence, this is the required solution.

Answer 2

The final speed of the rocket once the engine has fired is V= 25 m/s

Step-by-step explanation:

impulse = amount of movement

I= 3.5 kg*m/s

m= 140g = 0.14 kg

V= ?

I= m*V

I/m=V

V= 25 m/s = 90 km/h