Question

Two billiard balls of identical mass move toward each other. Assume that the collision between them is perfectly elastic. If the initial velocities of the balls are + 30.0 cm/s and -20.0 cm/s, what is the velocity of each ball after the collision? Assume friction and Rotation are unimportant.

Answer 1

As yo may know, in a perfectly elastic collision the kinetic energy remains constant; we have that:

K1 = (1/2)M*v1^2 = M*(30^2)/2

K2 = M*(-20^2)/2

Kt = k1 + k2 = M*650

Where M is the mass of the balls:

After the collision, (I denote the new quantities with an ' symbol) we must have the same energy:

K1' = (1/2)M(v1'^2 + v2'^2) = M650

v1'^2 + v2'^2 = 1300

And we also know that the total moment must be conserved:

M*30 - M*20 = M*10 = M( v1' + v2')

10 = v1' + v2'

Now we have two equations:

10 = v1' + v2'

v1'^2 + v2'^2 = 1300

We can writhe the first equation as:

10 - v1' = v2'

and replace it in the second equation:

v1'^2 + (10 - v1')^2 = 1300

and solve it for v1:

v1'^2 + 100 + v1^2 -20v1' - 1200 = 0

2*v1'^2 - 20v1' -1200 = 0

now we must solve this for v1 with the quadratic formula:

`v1' = (20 +/-√(20*20 - 4*2*-1400) )/(2*2)  = 5 +/- 25`

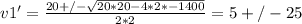
So we have two solutions:

v1' = (5 + 25)cm/s = 30cm/s

v1' = (5 - 20)cm/s = -20cm/s

and you can find that is the same case for v2' (interchanged, when v1' = 30cm/s we have that v2' = -20cm/s, and viseverce)

Now, after the impact, the first ball must change the direction of movement (It cant keep moving forward because there is the other ball in the path) so the velocities of the balls must be interchanged, this mens that v1' = -20cm/s and v2'= 30cm/s

Answer 2

-20.0 m/s and 30.0 m/s

Step-by-step explanation:

Momentum is conserved:

m (30.0) + m (-20.0) = m v₁ + m v₂

30.0 − 20.0 = v₁ + v₂

10.0 = v₁ + v₂

Since the collision is perfectly elastic, energy is also conserved. Since there's no rotational energy or work done by friction, the initial kinetic energy equals the final kinetic energy.

½ m (30.0)² + ½ m (-20.0)² = ½ mv₁² + ½ mv₂²

(30.0)² + (-20.0)² = v₁² + v₂²

1300 = v₁² + v₂²

We now have two equations and two variables. Solve the system of equations using substitution:

1300 = v₁² + (10 − v₁)²

1300 = v₁² + 100 − 20v₁ + v₁²

0 = 2v₁² − 20v₁ − 1200

0 = v₁² − 10v₁ − 600

0 = (v₁ + 20) (v₁ − 30)

v₁ = -20, 30

If v₁ = -20, v₂ = 30.

If v₁ = 30, v₂ = -20.

So either way, the final velocities are -20.0 m/s and 30.0 m/s.