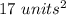Question

What is the area of triangleABC?

Answer 1

Option A.

The closest area of triangle ABC is
`17\ units^(2)`

Explanation:

In this problem

If sin(a)=cos(b)

then

Angles a and b are complementary

so

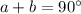`a+b=90\°`-----> equation A

therefore

The triangle ABC is a right triangle

step 1

Find the value of x

substitute the given values of a and b in the equation A

`(2x-15)\°+(5x-21)\°=90\°\\(7x-36)\°=90\°\\ 7x=90+36\\ x=18\°\\ a=(2x-15)\°=2(18)-15=21\°\\ b=(5x-21)\°=5(18)-21=69\°`

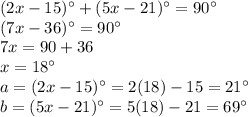
step 2

Find the length of side AC

we know that

In the right triangle ABC

`cos(a)=AC/BC\\ AC=(BC)cos(a)`

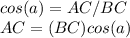
substitute the given values

`AC=(10)cos(21\°)=9.34\ units`

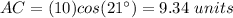
step 3

Find the length of side AB

we know that

In the right triangle ABC

`sin(a)=AB/BC\\ AB=(BC)sin(a)`

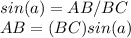
substitute the given values

`AB=(10)sin(21\°)=3.58\ units`

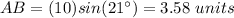
step 4

Find the area of triangle ABC

The area is equal to

`A=(1/2)(AB)(AC)`

substitute

`A=(1/2)(3.58)(9.34)=16.7\ units^(2)`

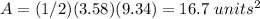
therefore

The closest area of triangle ABC is
`17\ units^(2)`