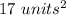Answer:
Option A.
The closest area of triangle ABC is
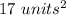
Explanation:
In this problem
If sin(a)=cos(b)
then
Angles a and b are complementary
so
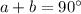 -----> equation A
-----> equation A
therefore
The triangle ABC is a right triangle
step 1
Find the value of x
substitute the given values of a and b in the equation A
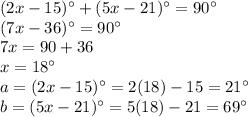
step 2
Find the length of side AC
we know that
In the right triangle ABC
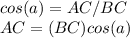
substitute the given values
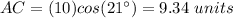
step 3
Find the length of side AB
we know that
In the right triangle ABC
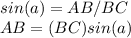
substitute the given values
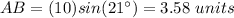
step 4
Find the area of triangle ABC
The area is equal to

substitute
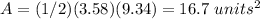
therefore
The closest area of triangle ABC is