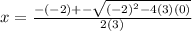Question

Which shows the correct substitution of values A, B, and C from the equation 1=-2x+3x^2+1 is the quadratic formula ?

Answer 1

Answer: A

Step-by-step explanation: Edge2023

Answer 2

`x=\frac{-(-2)+-\sqrt{(-2)^(2)-4(3)(0)}}{2(3)}`

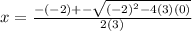
Explanation:

* Lets revise the general form of the quadratic equation

- The general form of the quadratic equation is Ax² + Bx + C = 0,

where A , B , C are constant

# A is the coefficient of x²

# B is the coefficient of x

# C is the numerical term

- The quadratic formula is
`x=\frac{-B+-\sqrt{B^(2)-4AC }}{2A}`

* Lets solve the problem

∵ 1 = -2x + 3x² + 1

- Subtract 1 from both side

∴ 0 = -2x + 3x²

- Switch the two sides

∴ -2x + 3x² = 0

- Arrange the equation from the greatest power of x to the smallest

∴ 3x² - 2x = 0

∵ A is the coefficient of x²

∴ A = 3

∵ B is the coefficient of x

∴ B = -2

∵ C is the numerical term

∵ There is no numerical term

∴ C = 0

- Substitute the values of A , B , C in the formula

∴
`x=\frac{-(-2)+-\sqrt{(-2)^(2)-4(3)(0)}}{2(3)}`