Question

Solve for x,y, and z

Answer 1

Part A)
`x=6`

Part B) ∠3=29°

Part C) ∠1=29°

Part D) ∠2=151°

Explanation:

Part A) If ∠3=5x-1 and ∠5=3x+11, then x=?

we know that

∠3=∠5 ----> by alternate interior angles

so

substitute and solve for x

`5x-1=3x+11`

`5x-3x=11+1`

`2x=12`

`x=6`

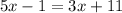
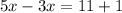
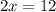
Part B) If ∠3=5x-1 and ∠5=3x+11, then the measure of ∠3=?

we know that

∠3=5x-1

The value of x is

`x=6`

substitute

∠3=5(6)-1=29°

Part C) If ∠3=5x-1 and ∠5=3x+11, then the measure of ∠1=?

we know that

∠1=∠3 ----> by vertical angles

we have

∠3=29°

therefore

∠1=29°

Part D) If ∠3=5x-1 and ∠5=3x+11, then the measure of ∠2=?

we know that

∠1+∠2=180° ----> by supplementary angles

we have

∠1=29°

substitute

29°+∠2=180°

∠2=180°-29°

∠2=151°