Question

a researcher wishes to estimate the proportion of adults who have high speed internet access. what size sample should be obtained if she wishes the estimate to be within 0.04 with 90% confidence if she uses a previous estimate of 0.54​

Answer 1

421

Explanation:

Margin of error = E = 0.04

Confidence Level = 90%

z value associated with this confidence level = z = 1.645

Previous estimate of population proportion = p = 0.54

q = 1 - p = 1 - 0.54 = 0.46

The formula of Margin of Error for population proportion is:

`E=z\sqrt{(pq)/(n)}`

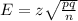
Here, n is the sample size.

Re-arranging the equation for n and using the values we get:

`n=((z)/(E))^(2) * pq\\\\ n = ((1.645)/(0.04))^(2) * 0.54 * 0.46\\\\ n = 421`

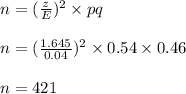
Thus the minimum sample size required to estimate the proportion of adults who have high speed internet access is 421