Question

In a geometric progression of positive terms, the 5th term is 9 times the 3rd term and the sum of the 6th and 7th terms is 972. Find the

a) common ratio
b) sum of the first 6 terms

Answer 1

a) 3

b) 364

Explanation:

A geometric sequence in explicit form is
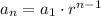`a_n=a_1 \cdot r^(n-1)` where
`a_1` is the first term and
`r` is the common ratio.

We are given:

`a_5=9 \cdot a_3`

`a_6+a_7=972`.

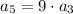
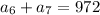What is a) r?

What is b) the sum of the first 6 terms?

So I'm going to use my first equation and use my explicit form to find those terms in terms of r:

`a_1 \cdot r^4=9 \cdot a_1 \cdot r^(2)`

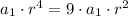
Divide both sides by
`a_1r^2`:

`r^2=9`

`r=√(9)`

`r=3`.

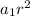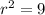
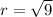
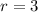So part a is 3.

Now for part b).

We want to find
`a_1+a_2+a_3+a_4+a_5+a_6`.

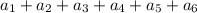So far we have:

`a_1=a_1`

`a_2=3a_1`

`a_3=3^2a_1`

`a_4=3^3a_1`

`a_5=3^4a_1`

`a_6=3^5a_1`.

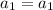
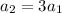
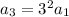
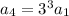
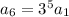We also haven't used:

`a_6+a_7=972`.

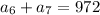I'm going to find these terms in terms of r (r=3).

`3^5a_1+3^6a_1=972`

`243a_1+729a_1=972`

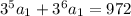
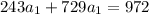
You have like terms to add:

`972a_1=972`

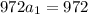
Divide both sides by 972:

`a_1=1`

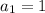
The first term is 1 and the common ratio is 3.

The terms we wrote can be simplify using a substitution for the first term as 1:

`a_1=a_1=1`

`a_2=3a_1=3(1)=3`

`a_3=3^2a_1=9(1)=9`

`a_4=3^3a_1=27(1)=27`

`a_5=3^4a_1=81(1)=81`

`a_6=3^5a_1=243(1)=243`.

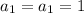
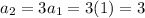
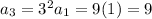
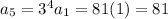
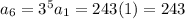Now we just need to find the sum of those six terms:

1+3+9+27+81+243=364.