Question

A system of inequalities can be used to determine the depth of a toy, in meters, in a pool depending on the time, in seconds, since it was dropped. Which constraint could be part of the scenario?

PLEASE ANSWER ASAP TIMED QUIZ

Answer 1

Answer:The Answer is A

Step-by-step explanation: I took the test on edge

Answer 2

The correct option is 1.

Explanation:

It is given that a system of inequalities can be used to determine the depth of a toy, in meters, in a pool depending on the time, in seconds, since it was dropped.

Let y be the depth of a toy and x is time, in seconds.

In the given graph a solid horizontal line passes through the point (0,-1) and shaded region is above the line. So, the inequality of red line is

`y\geq -1`

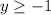
The depth of a toy can be less than -1. It means the pool is 1 meter deep.

The blue line is a dashed line which passes through (0,0) and (2,-1).

So the slope of line is

`m=(y_2-y_1)/(x_2-x_1)=(-1-0)/(2-0)=-(1)/(2)`

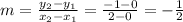
The equation of blue line is

`y=mx+b`

where, m is slope and b is y-intercept.

`y=-(1)/(2)x+0`

`y=-(1)/(2)x`

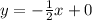
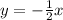
The shaded region is below the line so the required inequality is

`y< -(1)/(2)x`

it means the toy sinks at a rate of less than 1/2 meter per second.

Therefore the correct option is 1.