Question

How would you answer this math question please this is my last question

Answer 1

Shorter sides: 270 feet.

Larger side: 540 feet.

Greatest possible area: 145800 square feet.

Explanation:

So we need fencing around the garden except along the river.

The opposite sides of a rectangular are congruent.

So the sides perpendicular to the river in the picture are both of the same length, let's call it x. The length opposite the river is y.

So the perimeter excluding the side along the river is

x+x+y or 2x+y or 1080 is how much fencing we want.

So we have the equation:

2x+y=1080

The area of rectangle can be found by multiplying it's dimensions:

xy=A

We want to find the dimensions that provide us with the maximum area.

This is our area function so for:

A=xy

We need the area to be in terms of one variable.

Let's use our condition that 2x+y=1080.

2x+y=1080

Subtract 2x on both sides:

y=1080-2x

or

y=-2x+1080

We are going to plug this into:

`A=xy`

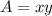
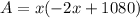`A=x(-2x+1080)` : I replaced y with -2x+1080 since y=-2x+1080.

`A=-2x^2+1080x` : I distribute.

Let's find the x-coordinate of the vertex.

To do this we need to determine
`a` and
`b` in the comparison of

`A=ax^2+bx+c`.

`a=-2`

`b=1080`

`c=0`

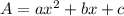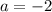
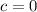
The formula for the x-coordinate of the vertex is
`(-b)/(2a)`.

`(-b)/(2a)=(-1080)/(2(-2))=(1080)/(4)=270`

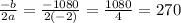
We could plug this into our area Area function in terms of to find maximum area.

We could also wait til later. I think I will do both for a later check.

`A=-2x^2+1080x` with
`x=270`

`A=-2(270)^2+1080(270)`

`A=145800`

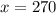
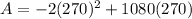
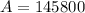
So we one dimension of the rectangle so for which is 270 feet.

We have the maximum area which is 145800 square feet.

Now recall y=-2x+1080.

y=-2x+1080 with x=270

y=-2(270)+1080

y=540

So we have one dimension of the rectangle is 270 feet.

Another dimension is 540 feet.

And the area of the rectangle is 145800 square feet.

Does 270(540) equal 145800? 270(540)=145800 so yes.

Let's check to see if we have 1080 feet of fencing.

So we have 2 small sides of 270 and 270 feet.

We have a larger side which is 540 feet.

270+270+540=10180 so everything checks out.