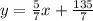Question

Write the equation of the line of best fit using the slope-intercept formula $y = mx + b$. Show all your work, including the points used to determine the slope and how the equation was determined.

Answer 1

`y=(5)/(7)x+(135)/(7)`

Explanation:

You only need two points on a line to find the equation for that line.

We are going to use 2 points that cross that line or at least come close to. You don't have to use the green points... just any point on the line will work. You might have to approximate a little.

I see ~(67.5,67.5) and ~(64,65).

Now once you have your points, we need to find the slope.

You may use
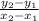`(y_2-y_1)/(x_2-x_1)` where
`(x_1,y_1) \text{ and } (x_2,y_2)` are points on the line.

Or you can line up the points vertically and subtract then put 2nd difference over 1st difference.

Like this:

( 64 , 65 )

-( 67.5, 67.5 )

--------------------

-3.5 -2.5

So the slope is -2.5/-3.5=2.5/3.5=25/35=5/7.

Now use point-slope form to find the equation:

`y-y_1=m(x-x_1)` where
`m` is the slope and
`(x_1,y_1)` is a point on the line.

`y-65=(5)/(7)(x-64)`

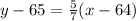
Distribute:

`y-65=(5)/(7)x-(5)/(7)\cdot 64`

Simplify:

`y-65=(5)/(7)x-(320)/(7)`

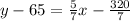
Add 65 on both sides:

`y=(5)/(7)x-(320)/(7)+65`

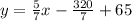
Simplify:

`y=(5)/(7)x+(135)/(7)`