Question

Question 3

1 pts
8 men and 6 women apply for a job at a new startup. How many
ways can 4 of the applicants be selected for a second interview?

Answer 1

1001 ways

Explanation:

Total number of people who applied for the job = 8 + 6 = 14

Number of people to be chosen = 4

This is a combination problem because the order of selection does not matter. A group selection involves the combinations. So here we have to find the combinations of 14 people taken 4 at a time. The formula for the combination is:

`^(n)C_(r) = (n!)/(r!(n-r)!)`

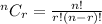
Here, n is the total number of objects which is 14 in this case.

r is the number of objects to be chosen which is 4 in this case.

Using these values, we get:

`^(14)C_(4)=(14!)/(4!(14-4)!)\\\\ = (14!)/(4! * 10!)\\\\ =1001`

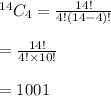
Thus, there are 1001 ways to select 4 applicants from 8 men and 6 women for the second interview.