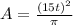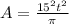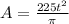The circumference of a circle is 30t. What is its area?

Question

asked Nov 9, 2020 203k views

1 Answer

Wxs · Answer 1 · 2020-11-13T14:08:42+0000

Answer:

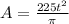$A=(225t^2)/(\pi)$ given the circumference is 30t.

Explanation:

The circumference of a circle is
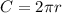$C=2\pi r$ and the area of a circle is
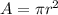$A=\pi r^2$ assuming the radius is
for the circle in question.

We are given the circumference of our circle is
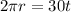$2 \pi r=30t$ .

If we solve this for r we get:
$r=(30t)/(2\pi)$ . To get this I just divided both sides by
$2\pi$ since this was the thing being multiplied to
.

So now the area is
$A=\pi r^2=\pi ((30t)/(2 \pi))^2$ .

Simplifying this:

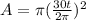$A=\pi ((30t)/(2 \pi))^2$ .

30/2=15 so:

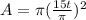$A=\pi ((15t)/(\pi))^2$ .

Squaring the numerator and the denominator:

$A=\pi (((15t)^2)/((\pi)^2)$

Using law of exponents or seeing that a factor of
$\pi$ cancels:

$A=((15t)^2)/(\pi)$

$A=(15^2t^2)/(\pi)$

$A=(225t^2)/(\pi)$