Question

Match the polygons formed by the set of points with their perimetersrounded to the nearest hundredth. Please help ASAP taking a test . Thank you so much in advance

Answer 1

Polygon ABCDE = 50 units

Polygon FGHIJ = 23.4 units

Polygon KLMNO = 19.24 units

Polygon UVWXY = 38 units

Explanation:

In order to find the perimeter, we have to find lengths of all sides of given points

The distance formula will be used to find the lengths

`d = \sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2) }`

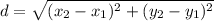
where (x_1,y_1) are coordinates of first point and (x_2,y_2) are coordinates of second point)

So,

For A(1,1), B(6,13), C(8,13), D(16,-2) and E(1, -2)

AB = 13 units

BC = 2 units

CD = 17 units

DE = 15 units

EA = 3 units

Perimeter of polygon ABCDE = 13+2+17+15+3 = 50 units

For F(14,-10), G(16,-10), H(19,-6), I(14,-2) and J(11,-6)

FG = 2 units

GH = 5 units

HI = 6.40 units

IJ = 5 units

JF = 5 units

Perimeter of polygon FGHIJ = 2+5+6.40+5+5 = 23.4 units

For K(4,2), L(8,2), M(12,5), N(6,5) and O(4,4)

KL = 4 units

LM = 5 units

MN = 6 units

NO = 2.24 units

OK = 2 units

Perimeter of polygon KLMNO = 4+5+6+2.24+2 = 19.24 units

For P(7,2), Q(12,2), R(12,6), S(7,10) and T(4,6)

PQ= 5 units

QR= 4 units

RS=6.40 units

ST= 5 units

TP = 5 units

Perimeter of polygon PQRST = 5+4+6.40+5+5 = 25.40 units

For U(4,-1), V(12, -1), W(20,-7), X(8, -7) and Y(4,-4)

UV = 8 units

VW = 10 units

WX = 12 units

XY = 5 units

YU = 3 units

Perimeter of polygon UVWXY = 8+10+12+5+3 = 38 units