Question

On a particular day, the wind added 4 miles per hour to Jaime's rate when she was rowing with the wind and subtracted 4 miles per hour from her rate on her return trip. Jaime found that in the same amount of time she could row 48 miles with the wind, she could go only 24 miles against the wind. What is her normal rowing speed with no wind?

Answer 1

12 miles per hour

Explanation:

Let her normal rowing speed be x

Also note the formula D = RT, where d is distance, R is rate(speed) and T is time

On windy day, her speed is x + 4

On against wind return, her speed is x - 4

With wind, she can go 48 miles in same amount of time when she goes 24 miles against wind. This can be written as:

48 = (x+4)T

24 = (x-4)T

We can write each equation in terms of T and equate both. So we have:

48/x+4 = T

24/x-4 = T

Thus,

`(48)/(x+4)=(24)/(x-4)\\48(x-4)=24(x+4)\\48x-192=24x+96\\24x=288\\x=(288)/(24)\\x=12`

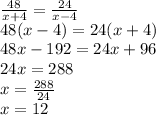
Thus, Jaime's normal rowing speed is 12 miles per hour