Answer:
 ,
,
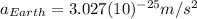
Explanation:
According to Newton’s law of universal gravitation, which is a classical physical law that describes the gravitational interaction between different bodies with mass:
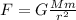 (1)
(1)
Where:
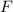 is the module of the force exerted between the apple and the Earth
is the module of the force exerted between the apple and the Earth
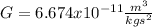 is the universal gravitation constant.
is the universal gravitation constant.
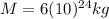 is the mass of the Earth and
is the mass of the Earth and
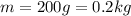 is the mass of the apple
is the mass of the apple
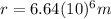 is the distance between the apple and the Earth (assuming tha apple is near the surface of the Earth)
is the distance between the apple and the Earth (assuming tha apple is near the surface of the Earth)
On the other hand, according Newton's 2nd Law of Motion the force
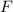 is directly proportional to the mass
is directly proportional to the mass
 and to the acceleration
and to the acceleration
 of a body.
of a body.
So, in the case of the apple:
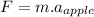 (2)
(2)
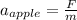 (3)
(3)
Substituting
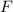 (1) in (3):
(1) in (3):
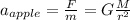 (4)
(4)
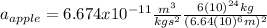 (5)
(5)
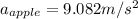 (6)
(6)
Now, in the case of the Earth:
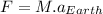 (7)
(7)
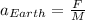 (8)
(8)
Substituting
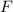 (1) in (8):
(1) in (8):
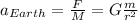 (9)
(9)
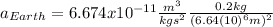 (10)
(10)
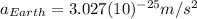 (11)
(11)
As we can see, the acceleration of the apple towards the Earth is greater than the acceleration of the Earth towards the apple (although the gravitational force between them is the same), because the mass of the Earth is greater than the mass of the apple.