Answer:
Graph the two points (0,1) and (2,-1) then connect them with a straight edge.
Explanation:
The transformed graph is still a line since the parent is a line.
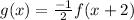
Identify two points that cross nicely on your curve for f:
(2,-2) and (4,2)
So I'm going to replace x in x+2 so that x+2 is 2 and then do it also for when x+2 is 4.
x+2=2 when x=0 since 0+2=2.
x+2=4 when x=2 since 2+2=4.
So plugging in x=0:
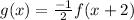
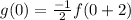

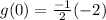 since we had the point (2,-2) on line f.
since we had the point (2,-2) on line f.
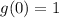 so g contains the point (0,1).
so g contains the point (0,1).
So plugging in the other value we had for x, x=2:
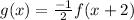
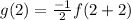
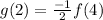
 since we had the point (4,2) on the line f.
since we had the point (4,2) on the line f.
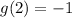 so g contains the point (2,-1).
so g contains the point (2,-1).
Graph the two points (0,1) and (2,-1) then connect them with a straight edge.