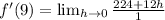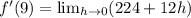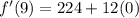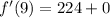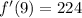Answer:
224
Explanation:
We will need the following rules for derivative:
 Sum rule.
Sum rule.
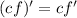 Constant multiple rule.
Constant multiple rule.
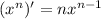 Power rule.
Power rule.
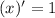 Slope of y=x is 1.
Slope of y=x is 1.
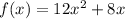
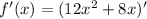
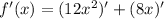 by sum rule.
by sum rule.
 by constant multiple rule.
by constant multiple rule.
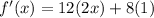 by power rule.
by power rule.

Now we need to find the derivative function evaluated at x=9.
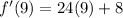
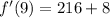
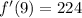
In case you wanted to use the formal definition of derivative:
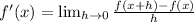
Or the formal definition evaluated at x=a:
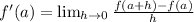
Let's use that a=9.
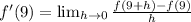
We need to find f(9+h) and f(9):

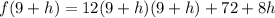
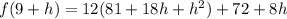
(used foil or the formula (x+a)(x+a)=x^2+2ax+a^2)
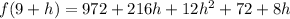
Combine like terms:

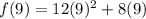
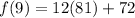
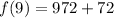
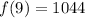
Ok now back to our definition:
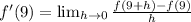
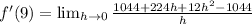
Simplify by doing 1044-1044:
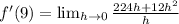
Each term has a factor of h so divide top and bottom by h: