Answer:
0.9317
Explanation:
Standard deviation of the weights =
 =100 lbs
=100 lbs
Mean weight = u = 1200 lbs
We need to find the probability that the weight(x) of a randomly selected steer is between 1000 lbs and 1369 lbs i.e. P(1000 < x < 1369)
Since, weights follow the normal distribution we can use the z values to find the required weight. For this we have to convert both the values to z score. The formula for z scores is:
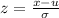
1000 converted to z scores is:
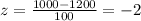
1369 converted to z scores is:
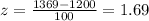
So, we have to find the values from z table that lie between -2 to 1.69
P( 1000 < x < 1369 ) = P(-2 < z < 1.69)
P(-2 < z < 1.69) = P(z < 1.69) - P(z < -2)
From the z table:
P(z < 1.69) = 0.9545
P(z < -2) = 0.0228
So,
P(-2 < z < 1.69) = 0.9545 - 0.0228 = 0.9317
Thus,
P( 1000 < x < 1369 ) = 0.9317
From this we can conclude that:
The probability that the weight of a randomly selected steer is between 1000 lbs and 1369 lbs is 0.9317