Question

Find an equation for the nth term of a geometric sequence where the second and fifth terms are -21 and 567, respectively.

Answer 1

`a_n=7 \cdot (-3)^(n-1)`

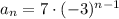
Explanation:

The explicit form for a geometric sequence is
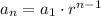`a_n=a_1 \cdot r^(n-1)` where
`a_1` is the first term and
`r` is the common ratio.

We have the following given:

`a_2=-21`

`a_5=567`.

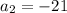
We also know that
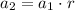`a_2=a_1 \cdot r` while
`a_5=a_1 \cdot r_4`.

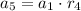So if we do 5th term divided by second term we get:

`(a_1 \cdot r_4)/(a_1 \cdot r)=(567)/(-21)`

Simplifying both sides:

`r^3=-27`

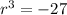
Cube root both sides:

`r=-3`

The common ratio, r, is -3.

Now we need to find the first term.

That shouldn't be too hard here since we know the second term which is -21.

We know that first term times the common ratio will give us the second term.

So we are solving the equation:

`a_1 \cdot r=a_2`.

`a_1 \cdot (-3)=-21`

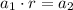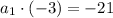
Dividing both sides by -3 gives us
`a_1=7`.

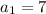So the equation is in it's explicit form is:

`a_n=7 \cdot (-3)^(n-1)`

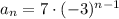
Check it!

Plugging in 2 should gives us a result of -21.

`a_2=7 \cdot (-3)^(2-1)`

`a_2=7 \cdot (-3)^1`

`a_2=7 \cdot (-3)`

`a_2=-21`

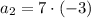
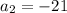
That checks out!

Plugging in 5 should give us a result of 567.

`a_5=7 \cdot (-3)^(5-1)`

`a_5=7 \cdot (-3)^4`

`a_5=7 \cdot 81`

`a_5=567`

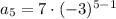
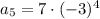
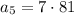
The checks out!

Our equation works!