Answer:
See explanation
Explanation:
Triangle ABC ha vertices at: A(-3,6), B(0,-4) and (2,6).
Let us apply 90 degrees clockwise about the origin twice to obtain 180 degrees clockwise rotation.
We apply the 90 degrees clockwise rotation rule.
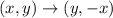
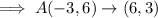


We apply the 90 degrees clockwise rotation rule again on the resulting points:
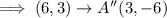
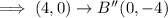
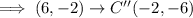
Let us now apply 90 degrees counterclockwise rotation about the origin twice to obtain 180 degrees counterclockwise rotation.
We apply the 90 degrees counterclockwise rotation rule.
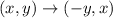

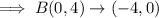
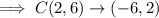
We apply the 90 degrees counterclockwise rotation rule again on the resulting points:
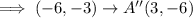
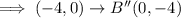
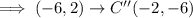
We can see that A''(3,-6), B''(0,-4) and C''(-2,-6) is the same for both the 180 degrees clockwise and counterclockwise rotations.