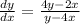Answer:
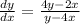
Explanation:
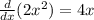
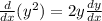
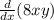
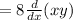
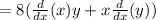
![=8[1y+x(dy)/(dx)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sksz1laqgdfiqlo3ph9zh8duo3jn1epjx3.png)
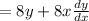
Let's put it altogether now:
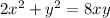
Differentiating both sides gives:
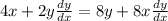
We are solving for dy/dx so we need to gather those terms on one side and the terms without on the opposing side:
I'm going to first subtract 4x on both sides:
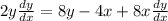
I'm not going to subtract 8xdy/dx on both sides:
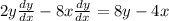
It is time to factor the dy/dx out of the two terms on the left:
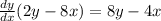
Divide both sides by (2y-8x):
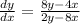
Reduce right hand side fraction: