Question

Solve the equation
log(5x)-log(x-3)=1​

Answer 1

x = 6

Explanation:

Using the rules of logarithms

• log x - log y ⇔ log (
`(x)/(y)` )

•
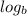`log_(b)` x = n ⇔ x =
`b^(n)`

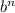
Given

log(5x) - log(x - 3) = 1

log (
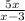`(5x)/(x-3)` ) = 1, then

`(5x)/(x-3)` =
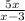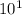`10^(1)` = 10 ( cross- multiply )

10(x - 3) = 5x

10x - 30 = 5x ( subtract 5x from both sides )

5x - 30 = 0 ( add 30 to both sides )

5x = 30 ( divide both sides by 5 )

x = 6

Answer 2

x =6

Explanation:

log(5x) - log(x - 3) = 1

Recall that the logarithm of a fraction is the difference of the logarithms,

so, the difference between two logarithms is logarithm of the fraction. Then,

`\begin{array}{rcll}\\\\\log (5x)/(x-3) & = & 1 &\\\\(5x)/(x - 3) & = & 10 & \text{Took the antilogarithm of each side}\\\\5x & = & 10(x - 3) & \text{Multiplied each side by x - 3}\\5x & = & 10x - 30 & \text{Distributed the 10}\\-5x & = & -30 & \text{Subtracted 10 x from each side}\\x & = & \mathbf{6} & \text{Divided each side by -5}\\\end{array}`

Check:

`\begin{array}{rcl}\log(5*6) - \log (6 - 3) & = & 1\\\log 30 - \log 3 & = &1\\\\\log (30)/(3) & = & 1\\\\\log 10 & = & 1\\1 & = & 1\\\end{array}`

OK.